distributing n balls in m boxes The term 'n balls in m boxes' refers to a combinatorial problem that explores how to distribute n indistinguishable balls into m distinguishable boxes.
When I started as an electrician in the mid 70s, the code stated that for metallic boxes, you had to ground to the box but for non-metallic boxes (at that time they were still "bakelite"), you had to ground devices that "required grounding".
0 · probability of m and n balls
1 · n balls vs m box probability
2 · n balls and m boxes
3 · math 210 distribution balls
4 · how to distribute n boxes
5 · how to distribute k balls into boxes
6 · distribution of balls into boxes pdf
7 · distributing balls to boxes
Find Sheet metal sheet metal at Lowe's today. Shop sheet metal and a variety of hardware products online at Lowes.com.
So the number of ways to distribute N balls into m boxes is: $$m^N$$ If we want to distribute N numbered balls into m boxes leaving the i-th box empty, each ball can only go to the m-1 .$$\binom{n}m=\binom{n-1}m+\binom{n-1}{m-1}$$ with the initial conditions .
Through some research I found that the answer is $\Omega = \binom{M+N-1}{N .Distributing k distinguishable balls into n distinguishable boxes, without exclusion, corresponds to forming a permutation of size k, with unrestricted repetitions, taken from a set of size n. .
$$\binom{n}m=\binom{n-1}m+\binom{n-1}{m-1}$$ with the initial conditions $\binom{n}0=1$ for all integers $n\ge 0$ and $\binom0m=0$ for all integers $m>0$. Added: To see why your .The term 'n balls in m boxes' refers to a combinatorial problem that explores how to distribute n indistinguishable balls into m distinguishable boxes.Through some research I found that the answer is $\Omega = \binom{M+N-1}{N-1}$ But why? I found an explanation which explained it like this: Let the balls be $\circ$. To find out how the .The balls into bins (or balanced allocations) problem is a classic problem in probability theory that has many applications in computer science. The problem involves m balls and n boxes (or .
The number of ways to place n balls into m boxes can be calculated using the formula n^m (n raised to the power of m). This formula assumes that each ball can be placed .
Assuming we have M identical boxes and N identical balls, we distribute these N balls among the M boxes in some way. Then we start removing balls (without replacement) .
Suppose there are n n identical objects to be distributed among r r distinct bins. This can be done in precisely \binom {n+r-1} {r-1} (r−1n+r−1) ways. Modeled as stars and bars, there are n n stars in a line and r-1 r −1 bars that divide them . The multinomial coefficient gives you the number of ways to order identical balls between baskets when grouped into a specific grouping (for example, 4 balls grouped into 3, 1, .So the number of ways to distribute N balls into m boxes is: $$m^N$$ If we want to distribute N numbered balls into m boxes leaving the i-th box empty, each ball can only go to the m-1 remaining boxes.Distributing k distinguishable balls into n distinguishable boxes, without exclusion, corresponds to forming a permutation of size k, with unrestricted repetitions, taken from a set of size n. Therefore, there are nk different ways to distribute k distinguishable balls into n distinguishable boxes, without exclusion. Case 3
$$\binom{n}m=\binom{n-1}m+\binom{n-1}{m-1}$$ with the initial conditions $\binom{n}0=1$ for all integers $n\ge 0$ and $\binom0m=0$ for all integers $m>0$. Added: To see why your reasoning doesn’t work, consider the case of $ balls and $ buckets, labelled $A$ and $B$.The term 'n balls in m boxes' refers to a combinatorial problem that explores how to distribute n indistinguishable balls into m distinguishable boxes.Through some research I found that the answer is $\Omega = \binom{M+N-1}{N-1}$ But why? I found an explanation which explained it like this: Let the balls be $\circ$. To find out how the balls are distributed in the boxes we use $N-1$ "|".The balls into bins (or balanced allocations) problem is a classic problem in probability theory that has many applications in computer science. The problem involves m balls and n boxes (or "bins"). Each time, a single ball is placed into one of the bins.
The number of ways to place n balls into m boxes can be calculated using the formula n^m (n raised to the power of m). This formula assumes that each ball can be placed in any of the m boxes, and that order does not matter. Assuming we have M identical boxes and N identical balls, we distribute these N balls among the M boxes in some way. Then we start removing balls (without replacement) according to the following rules: First, we observe which boxes contain balls.Suppose there are n n identical objects to be distributed among r r distinct bins. This can be done in precisely \binom {n+r-1} {r-1} (r−1n+r−1) ways. Modeled as stars and bars, there are n n stars in a line and r-1 r −1 bars that divide them into r r distinct groups.

The multinomial coefficient gives you the number of ways to order identical balls between baskets when grouped into a specific grouping (for example, 4 balls grouped into 3, 1, and 1 - in this case M=4 and N=3).So the number of ways to distribute N balls into m boxes is: $$m^N$$ If we want to distribute N numbered balls into m boxes leaving the i-th box empty, each ball can only go to the m-1 remaining boxes.Distributing k distinguishable balls into n distinguishable boxes, without exclusion, corresponds to forming a permutation of size k, with unrestricted repetitions, taken from a set of size n. Therefore, there are nk different ways to distribute k distinguishable balls into n distinguishable boxes, without exclusion. Case 3
$$\binom{n}m=\binom{n-1}m+\binom{n-1}{m-1}$$ with the initial conditions $\binom{n}0=1$ for all integers $n\ge 0$ and $\binom0m=0$ for all integers $m>0$. Added: To see why your reasoning doesn’t work, consider the case of $ balls and $ buckets, labelled $A$ and $B$.The term 'n balls in m boxes' refers to a combinatorial problem that explores how to distribute n indistinguishable balls into m distinguishable boxes.
probability of m and n balls
n balls vs m box probability
Through some research I found that the answer is $\Omega = \binom{M+N-1}{N-1}$ But why? I found an explanation which explained it like this: Let the balls be $\circ$. To find out how the balls are distributed in the boxes we use $N-1$ "|".
The balls into bins (or balanced allocations) problem is a classic problem in probability theory that has many applications in computer science. The problem involves m balls and n boxes (or "bins"). Each time, a single ball is placed into one of the bins. The number of ways to place n balls into m boxes can be calculated using the formula n^m (n raised to the power of m). This formula assumes that each ball can be placed in any of the m boxes, and that order does not matter.
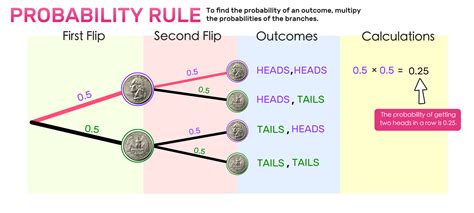
n balls and m boxes
Assuming we have M identical boxes and N identical balls, we distribute these N balls among the M boxes in some way. Then we start removing balls (without replacement) according to the following rules: First, we observe which boxes contain balls.
math 210 distribution balls
Suppose there are n n identical objects to be distributed among r r distinct bins. This can be done in precisely \binom {n+r-1} {r-1} (r−1n+r−1) ways. Modeled as stars and bars, there are n n stars in a line and r-1 r −1 bars that divide them into r r distinct groups.
how to distribute n boxes

Activate the Junction Boxes. With the Electric active, aim at the box and hit it to power it up, and let Officer Davis in.
distributing n balls in m boxes|how to distribute k balls into boxes